While working on an implementation of merge sort promised in the previous article, I realized that I'd like to use one neat little thing, which is worth its own post. It is a simple strategy for sorting or doing comparison-based tasks, which works wonderfully when input data is small enough.
Suppose that we have a very small array and we want to sort it as fast as possible. Indeed, applying some fancy O(N log N) algorithm is not a good idea: although it has optimal asymptotic performance, its logic is too complicated to outperform simple bubble-sort-like algorithms which take O(N^2) time instead. That's why every well-optimized sorting algorithm based on quicksort (e.g. std::sort) or mergesort includes some simple quadratic algorithm which is run for sufficiently small subarrays like N <= 32.
What exactly should we strive for to get an algorithm efficient for small N? Here is the list of things to look for:
- Avoid branches whenever possible: unpredictable ones are very slow.
- Reduce data dependency: this allows to fully utilize processing units in CPU pipeline.
- Prefer simple data access and manipulation patterns: this allows to vectorize the algorithm.
- Avoid complicated algorithms: they almost always fail on one of the previous points, and they sometimes do too much work for small inputs.
I decided to start investigating a simpler problem first, which is solved by std::lower_bound: given a sorted array of elements and a key, find index of the first array element greater or equal than the key. And this investigation soon developed into a full-length standalone article.
Binary search
The problem is typically solved with binary search in O(log N) time, but it might easily happen so that for small N simple linear algorithm would be faster. Of course, not all implementations of binary search are created equal: for small arrays branchless implementation is preferred. You can read about it for instance in this demofox's blog post. Here is a branchless implementation that we will use in the comparison later:
int binary_search_branchless (const int *arr, int n, int key) {
intptr_t pos = -1;
intptr_t logstep = bsr(n);
intptr_t step = intptr_t(1) << logstep;
while (step > 0) {
pos = (arr[pos + step] < key ? pos + step : pos);
step >>= 1;
}
return pos + 1;
}
This code only works properly when N+1 is power of two.
In order to support arbitrary size of input array, some sort of modification is required. The best approach for it is described in this blog post from Paul Khuong, which is: make the very first iteration special by using step = n+1 - 2^logstep instead of just 2^logstep, so that regardless of comparison result the next search interval would have length 2^logstep, including either the beginning of array or the end of array (note that two such possible intervals overlap, and this is not a problem).
The comparison itself is included in the ternary operator, which is supposed to compile into cmovXX instruction. And it really happens (unless your compiler thinks that you compile for 486), according to assembly listing of the innermost loop:
$LL491@main:
lea rax, QWORD PTR [rcx+rdx]
cmp DWORD PTR [rdi+rax*4], r8d
cmovl rdx, rax
sar rcx, 1
test rcx, rcx
jg SHORT $LL491@main
How good is this binary search implementation? It has no branches (point 1 from the above list), which is great. But it is inherently sequental (point 2): you cannot know which element to load on the next step until the element on the current step has been loaded and compared completely. Data access is scalar (point 3): you cannot vectorize it even if several keys are searched simultaneously.
We can take closer look by using Intel Architecture Code Analyzer: IACA is a small static analysis tool, which analyzes a snippet of code at instruction level. It assumes that the code piece is run in the infinite loop, that all branches are well-predicted and not taken, and that all memory accesses hit L1 cache (plus maybe some other assumptions). It is somewhat tricky to use with Visual C++ 64-bit compiler: you have to copy-paste the piece of code from assembly listing, surround it with markers (which are a bit wrong in iacaMarks.h by the way), then compile it with ml64.exe, and pass the resulting object file into iaca.exe.
Here is what IACA says about the innermost loop:
Throughput Analysis Report
--------------------------
Block Throughput: 2.15 Cycles Throughput Bottleneck: Dependency chains (possibly between iterations)
Port Binding In Cycles Per Iteration:
---------------------------------------------------------------------------------------
| Port | 0 - DV | 1 | 2 - D | 3 - D | 4 | 5 | 6 | 7 |
---------------------------------------------------------------------------------------
| Cycles | 1.5 0.0 | 0.9 | 0.5 0.5 | 0.5 0.5 | 0.0 | 1.1 | 1.5 | 0.0 |
---------------------------------------------------------------------------------------
| Num Of | Ports pressure in cycles | |
| Uops | 0 - DV | 1 | 2 - D | 3 - D | 4 | 5 | 6 | 7 | |
---------------------------------------------------------------------------------
| 1 | | 0.3 | | | | 0.6 | | | | lea rax, ptr [rdx+rcx*1]
| 2 | | 0.6 | 0.5 0.5 | 0.5 0.5 | | 0.4 | | | | cmp dword ptr [rdi+rax*4], r8d
| 1 | 0.4 | | | | | | 0.6 | | | cmovl rdx, rax
| 1 | 0.5 | | | | | | 0.5 | | CP | sar rcx, 0x1
| 1 | 0.6 | | | | | | 0.4 | | CP | test rcx, rcx
| 0F | | | | | | | | | | jnle 0xffffffffffffffee
Total Num Of Uops: 6
So it says that bottleneck is "dependency chains" and it estimates single iteration of the loop in 2.15 cycles. The estimate is clearly wrong: it is easy to see that the first three instructions must be executed sequentally, and the first of them cannot start before that last of them from the previous iterations has finished. A load from L1 costs 4 cycles latency-wise, address generation and other three instructions take at least 1 cycle each. So the innermost loop should take 8 cycles per iteration. If we look how performance measurements increase from doubling N, we can estimate one iteration in 4-5 cycles throughput and 10 cycles latency: both are much greater that the estimate given by IACA.
Since the loop in the binary search is very small (4-6 microops) and it goes for tiny number of iterations (e.g. 6 iterations for N = 64), one might suspect that the loop itself can take considerable time. That's why I have also implemented fully unrolled version of branchess binary search:
template<intptr_t MAXN> int binary_search_branchless_UR(const int *arr, int n, int key) {
assert(n+1 == MAXN);
intptr_t pos = -1;
#define STEP(logstep) \
if ((1<<logstep) < MAXN) \
pos = (arr[pos + (1<<logstep)] < key ? pos + (1<<logstep) : pos);
STEP(9)
STEP(8)
STEP(7)
STEP(6)
STEP(5)
STEP(4)
STEP(3)
STEP(2)
STEP(1)
STEP(0)
#undef STEP
return pos + 1;
}
This is of course quite far from the code usable in real programming, but it allows us to ignore all the overhead from the binary search and look directly at its core. IACA provides the following information about the code of the function (N = 64):
Throughput Analysis Report
--------------------------
Block Throughput: 29.00 Cycles Throughput Bottleneck: Dependency chains (possibly between iterations)
Port Binding In Cycles Per Iteration:
---------------------------------------------------------------------------------------
| Port | 0 - DV | 1 | 2 - D | 3 - D | 4 | 5 | 6 | 7 |
---------------------------------------------------------------------------------------
| Cycles | 5.0 0.0 | 5.0 | 3.0 3.0 | 3.0 3.0 | 0.0 | 5.0 | 5.0 | 0.0 |
---------------------------------------------------------------------------------------
| Num Of | Ports pressure in cycles | |
| Uops | 0 - DV | 1 | 2 - D | 3 - D | 4 | 5 | 6 | 7 | |
---------------------------------------------------------------------------------
| 1* | | | | | | | | | | mov r9, rcx
| 1 | | 1.0 | | | | | | | | mov eax, 0x1f
| 1 | | | | | | 1.0 | | | | or rcx, 0xffffffffffffffff
| 2^ | | | 1.0 1.0 | | | | 1.0 | | CP | cmp dword ptr [r9+0x7c], r8d
| 1 | 1.0 | | | | | | | | CP | cmovnl rax, rcx
| 2 | | 1.0 | | 1.0 1.0 | | | | | CP | cmp dword ptr [r9+rax*4+0x40], r8d
| 1 | | | | | | 1.0 | | | | lea rdx, ptr [rax+0x10]
| 1 | 1.0 | | | | | | | | CP | cmovnl rdx, rax
| 2 | | | 1.0 1.0 | | | | 1.0 | | CP | cmp dword ptr [r9+rdx*4+0x20], r8d
| 1 | | 1.0 | | | | | | | | lea rax, ptr [rdx+0x8]
| 1 | 1.0 | | | | | | | | CP | cmovnl rax, rdx
| 2 | | | | 1.0 1.0 | | 1.0 | | | CP | cmp dword ptr [r9+rax*4+0x10], r8d
| 1 | | 1.0 | | | | | | | | lea rcx, ptr [rax+0x4]
| 1 | | | | | | | 1.0 | | CP | cmovnl rcx, rax
| 2 | | | 1.0 1.0 | | | 1.0 | | | CP | cmp dword ptr [r9+rcx*4+0x8], r8d
| 1 | | 1.0 | | | | | | | | lea rdx, ptr [rcx+0x2]
| 1 | 1.0 | | | | | | | | CP | cmovnl rdx, rcx
| 2 | | | | 1.0 1.0 | | | 1.0 | | CP | cmp dword ptr [r9+rdx*4+0x4], r8d
| 1 | | | | | | 1.0 | | | | lea rax, ptr [rdx+0x1]
| 1 | 1.0 | | | | | | | | CP | cmovnl rax, rdx
| 1 | | | | | | | 1.0 | | CP | inc rax
Total Num Of Uops: 27
It is hard to say how IACA got 29 cycles per search. The critical path is marked properly: groups of cmov and cmp must go sequentally after each other, each group taking 7 cycles latency-wise, so latency of the whole code should be about 42 cycles. In the benchmark, the whole search takes 21 cycles throughput and 59 cycles latency, while doubling N adds 4-5 cycles more throughput and 8-9 cycles more latency. It seems that CPU manages to execute several consecutive searches in parallel thanks to pipelining, that's why throughput time is lower than latency time for branchless binary searches.
I believe this is the best you can get from a binary search.
Linear search
Things start to get more interesting when we try to invent a simple search algorithm working in O(N) time. Because there are actually several ways to do so. If you look the question "How fast can you make linear search?" on stackoverflow, you will see a basic code like this:
int linearX_search_scalar (const int *arr, int n, int key) {
intptr_t i = 0;
while (i < n) {
if (arr[i] >= key)
break;
++i;
}
return i;
}
Most of the answers for the question are just optimized versions of this algorithm: even if they compare more than one element at a time (with SSE), they still break out when the desired element is found. For instance, the author of the question (Schani) suggests the following code in his blog post:
int linearX_search_sse (const int *arr, int n, int key) {
__m128i *in_data = (__m128i*)arr;
__m128i key4 = _mm_set1_epi32(key);
intptr_t i = 0;
int res;
for (;;) {
__m128i cmp0 = _mm_cmpgt_epi32(key4, in_data [i + 0]);
__m128i cmp1 = _mm_cmpgt_epi32(key4, in_data [i + 1]);
__m128i cmp2 = _mm_cmpgt_epi32(key4, in_data [i + 2]);
__m128i cmp3 = _mm_cmpgt_epi32(key4, in_data [i + 3]);
__m128i pack01 = _mm_packs_epi32(cmp0, cmp1);
__m128i pack23 = _mm_packs_epi32(cmp2, cmp3);
__m128i pack0123 = _mm_packs_epi16 (pack01, pack23);
res = _mm_movemask_epi8 (pack0123);
if (res != 0xFFFF)
break;
i += 4;
}
return i * 4 + bsf(~res);
}
This code has no issues from the list of things that may slow down the algorithm, except for one mispredicted branch. The branch which checks if the answer is found is never taken except for the very last iteration when the loop terminates (which may happen at random moment). Of course, single misprediction is not a problem in a long loop, but it may cause problems when we want to optimize a tiny loop. In fact, Paul Khuong's blog post claims that linear search is always slower than branchless binary search because of this single mispredicted branch. Luckily, there is a way to avoid branches completely.
The idea is very simple: the sought-for index is precisely the number of elements in the array which are less than the key you search for. In fact, this criterion would work the same way even if you shuffle the input array randomly =) Here is the scalar implementation based on this criterion:
int linear_search_scalar (const int *arr, int n, int key) {
int cnt = 0;
for (int i = 0; i < n; i++)
cnt += (arr[i] < key);
return cnt;
}
For a vectorized implementation, we can compare a pack of four elements with the key, and then subtract the resulting masks (recall that they are -1 when comparison result is true) from the common accumulator. At the end we have to compute horizontal sum of the accumulator to get the total count. Finally, it is better to process several packs during single iteration (similar to unrolling) to reduce loop overhead. Here is the code:
int linear_search_sse (const int *arr, int n, int key) {
__m128i vkey = _mm_set1_epi32(key);
__m128i cnt = _mm_setzero_si128();
for (int i = 0; i < n; i += 16) {
__m128i mask0 = _mm_cmplt_epi32(_mm_load_si128((__m128i *)&arr[i+0]), vkey);
__m128i mask1 = _mm_cmplt_epi32(_mm_load_si128((__m128i *)&arr[i+4]), vkey);
__m128i mask2 = _mm_cmplt_epi32(_mm_load_si128((__m128i *)&arr[i+8]), vkey);
__m128i mask3 = _mm_cmplt_epi32(_mm_load_si128((__m128i *)&arr[i+12]), vkey);
__m128i sum = _mm_add_epi32(_mm_add_epi32(mask0, mask1), _mm_add_epi32(mask2, mask3));
cnt = _mm_sub_epi32(cnt, sum);
}
cnt = _mm_add_epi32(cnt, _mm_shuffle_epi32(cnt, SHUF(2, 3, 0, 1)));
cnt = _mm_add_epi32(cnt, _mm_shuffle_epi32(cnt, SHUF(1, 0, 3, 2)));
return _mm_cvtsi128_si32(cnt);
}
It requires the input array to be padded with sentinel elements INT_MAX until its size becomes divisible by 16. This requirement may be lifted by processing at most 15 last elements with additional loop(s), but I suppose such a version would work somewhat slower than the version with sentinels.
IACA provides the following info for the innermost loop of the code:
Throughput Analysis Report
--------------------------
Block Throughput: 5.05 Cycles Throughput Bottleneck: Dependency chains (possibly between iterations)
Port Binding In Cycles Per Iteration:
---------------------------------------------------------------------------------------
| Port | 0 - DV | 1 | 2 - D | 3 - D | 4 | 5 | 6 | 7 |
---------------------------------------------------------------------------------------
| Cycles | 0.5 0.0 | 4.5 | 2.0 2.0 | 2.0 2.0 | 0.0 | 4.5 | 0.5 | 0.0 |
---------------------------------------------------------------------------------------
| Num Of | Ports pressure in cycles | |
| Uops | 0 - DV | 1 | 2 - D | 3 - D | 4 | 5 | 6 | 7 | |
---------------------------------------------------------------------------------
| 2^ | | 0.5 | 1.0 1.0 | | | 0.5 | | | | vpcmpgtd xmm1, xmm3, xmmword ptr [rcx-0x20]
| 2^ | | 0.5 | | 1.0 1.0 | | 0.5 | | | | vpcmpgtd xmm0, xmm3, xmmword ptr [rcx-0x10]
| 1 | | 0.5 | | | | 0.5 | | | CP | lea rcx, ptr [rcx+0x40]
| 1 | | 0.5 | | | | 0.5 | | | | vpaddd xmm2, xmm1, xmm0
| 2^ | | 0.5 | 1.0 1.0 | | | 0.5 | | | CP | vpcmpgtd xmm1, xmm3, xmmword ptr [rcx-0x30]
| 2^ | | 0.5 | | 1.0 1.0 | | 0.5 | | | CP | vpcmpgtd xmm0, xmm3, xmmword ptr [rcx-0x40]
| 1 | | 0.5 | | | | 0.5 | | | CP | vpaddd xmm1, xmm1, xmm0
| 1 | | 0.5 | | | | 0.5 | | | CP | vpaddd xmm2, xmm2, xmm1
| 1 | | 0.5 | | | | 0.5 | | | CP | vpsubd xmm4, xmm4, xmm2
| 1 | 0.5 | | | | | | 0.5 | | | sub rdx, 0x1
| 0F | | | | | | | | | | jnz 0xffffffffffffffd4
Total Num Of Uops: 14
And again: I'm not sure how IACA got 5.05 cycles per iteration. Most of the work done each iteration is clearly independent between iterations, so in a theoretical infinite loop several consecutive iterations can be executed in parallel, thus hiding latency of memory loads and dependencies. As for performance measurements, going from 64 elements to 128 elements increases time by 12.4 ns, which is 6.2 cycles per iteration. The cost per iteration decreases to 5.5 cycles for larger N. Note that both latency and throughput measurements increase equally with increase of N, which confirms the fact that iterations are processed independently. Given that execution ports pressure is 4.5 cycles per iteration, spending 5.5 cycles is pretty efficient usage of hardware (compared to binary search).
To make sure loop overhead is not critical, I have also implemented fully unrolled version of this vectorized implementation. For N = 64 it has four iterations unrolled, and here is its assembly code analyzed by IACA:
Throughput Analysis Report
--------------------------
Block Throughput: 19.25 Cycles Throughput Bottleneck: FrontEnd, Port1, Port5
Port Binding In Cycles Per Iteration:
---------------------------------------------------------------------------------------
| Port | 0 - DV | 1 | 2 - D | 3 - D | 4 | 5 | 6 | 7 |
---------------------------------------------------------------------------------------
| Cycles | 1.0 0.0 | 18.8 | 8.0 8.0 | 8.0 8.0 | 0.0 | 19.3 | 0.0 | 0.0 |
---------------------------------------------------------------------------------------
| Num Of | Ports pressure in cycles | |
| Uops | 0 - DV | 1 | 2 - D | 3 - D | 4 | 5 | 6 | 7 | |
---------------------------------------------------------------------------------
| 1* | | | | | | | | | | vpxor xmm3, xmm3, xmm3
| 1 | | | | | | 1.0 | | | CP | vmovd xmm5, r8d
| 1 | | | | | | 1.0 | | | CP | vpbroadcastd xmm5, xmm5
| 2^ | | 0.9 | 1.0 1.0 | | | 0.1 | | | CP | vpcmpgtd xmm1, xmm5, xmmword ptr [rcx+0x30]
| 2^ | | 0.8 | | 1.0 1.0 | | 0.3 | | | CP | vpcmpgtd xmm0, xmm5, xmmword ptr [rcx+0x20]
| 1 | | 0.5 | | | | 0.5 | | | CP | vpaddd xmm2, xmm1, xmm0
| 2^ | | 0.6 | 1.0 1.0 | | | 0.4 | | | CP | vpcmpgtd xmm0, xmm5, xmmword ptr [rcx]
| 2^ | | 0.4 | | 1.0 1.0 | | 0.6 | | | CP | vpcmpgtd xmm1, xmm5, xmmword ptr [rcx+0x10]
| 1 | | 0.6 | | | | 0.4 | | | CP | vpaddd xmm1, xmm1, xmm0
| 2^ | | 0.4 | 1.0 1.0 | | | 0.6 | | | CP | vpcmpgtd xmm0, xmm5, xmmword ptr [rcx+0x60]
| 1 | | 0.6 | | | | 0.4 | | | CP | vpaddd xmm2, xmm2, xmm1
| 2^ | | 0.4 | | 1.0 1.0 | | 0.6 | | | CP | vpcmpgtd xmm1, xmm5, xmmword ptr [rcx+0x70]
| 1 | | 0.6 | | | | 0.4 | | | CP | vpsubd xmm4, xmm3, xmm2
| 1 | | 0.4 | | | | 0.6 | | | CP | vpaddd xmm2, xmm1, xmm0
| 2^ | | 0.6 | 1.0 1.0 | | | 0.4 | | | CP | vpcmpgtd xmm0, xmm5, xmmword ptr [rcx+0x40]
| 2^ | | 0.4 | | 1.0 1.0 | | 0.6 | | | CP | vpcmpgtd xmm1, xmm5, xmmword ptr [rcx+0x50]
| 1 | | 0.6 | | | | 0.4 | | | CP | vpaddd xmm1, xmm1, xmm0
| 2^ | | 0.4 | 1.0 1.0 | | | 0.6 | | | CP | vpcmpgtd xmm0, xmm5, xmmword ptr [rcx+0xa0]
| 1 | | 0.6 | | | | 0.4 | | | CP | vpaddd xmm2, xmm2, xmm1
| 2^ | | 0.4 | | 1.0 1.0 | | 0.6 | | | CP | vpcmpgtd xmm1, xmm5, xmmword ptr [rcx+0xb0]
| 1 | | 0.6 | | | | 0.4 | | | CP | vpsubd xmm3, xmm4, xmm2
| 1 | | 0.4 | | | | 0.6 | | | CP | vpaddd xmm2, xmm1, xmm0
| 2^ | | 0.6 | 1.0 1.0 | | | 0.4 | | | CP | vpcmpgtd xmm0, xmm5, xmmword ptr [rcx+0x80]
| 2^ | | 0.4 | | 1.0 1.0 | | 0.6 | | | CP | vpcmpgtd xmm1, xmm5, xmmword ptr [rcx+0x90]
| 1 | | 0.6 | | | | 0.4 | | | CP | vpaddd xmm1, xmm1, xmm0
| 2^ | | 0.4 | 1.0 1.0 | | | 0.6 | | | CP | vpcmpgtd xmm0, xmm5, xmmword ptr [rcx+0xe0]
| 1 | | 0.6 | | | | 0.4 | | | CP | vpaddd xmm2, xmm2, xmm1
| 2^ | | 0.4 | | 1.0 1.0 | | 0.6 | | | CP | vpcmpgtd xmm1, xmm5, xmmword ptr [rcx+0xf0]
| 1 | | 0.6 | | | | 0.4 | | | CP | vpsubd xmm4, xmm3, xmm2
| 1 | | 0.4 | | | | 0.6 | | | CP | vpaddd xmm2, xmm1, xmm0
| 2^ | | 0.6 | 1.0 1.0 | | | 0.4 | | | CP | vpcmpgtd xmm0, xmm5, xmmword ptr [rcx+0xc0]
| 2^ | | 0.4 | | 1.0 1.0 | | 0.6 | | | CP | vpcmpgtd xmm1, xmm5, xmmword ptr [rcx+0xd0]
| 1 | | 0.6 | | | | 0.4 | | | CP | vpaddd xmm1, xmm1, xmm0
| 1 | | 0.4 | | | | 0.6 | | | CP | vpaddd xmm2, xmm2, xmm1
| 1 | | 0.6 | | | | 0.4 | | | CP | vpsubd xmm3, xmm4, xmm2
| 1 | | | | | | 1.0 | | | CP | vpshufd xmm0, xmm3, 0x4e
| 1 | | 1.0 | | | | | | | CP | vpaddd xmm2, xmm0, xmm3
| 1 | | | | | | 1.0 | | | CP | vpshufd xmm1, xmm2, 0xb1
| 1 | | 1.0 | | | | | | | CP | vpaddd xmm0, xmm1, xmm2
| 1 | 1.0 | | | | | | | | | vmovd eax, xmm0
Total Num Of Uops: 56
The broadwell execution ports 1 and 5 are fully saturated here, the beginning and the ending of the function take about 3 cycles throughput, so there is about 16 cycles spent on the middle part, which gives about 4 cycles per loop iteration (i.e. per 16 elements). Performance measurements fully confirm this estimate: going from 64 to 128 elements increases time by 8.3 ns, which is 4.15 cycles per iteration. For larger N, cost per loop iteration perfectly converges to 4 cycles. These statements are true both for throughput and latency performance.
Finally, I have implemented AVX versions of the same algorithm (both in a loop and fully unrolled). They would also be present in comparison.
Comparison
The testing code works as follows. Both keys and input elements are generated randomly and uniformly between 0 and N+1. The input array always has size N in form 2^k-1, not including one sentinel element INT_MAX. Several input arrays and several keys for search are generated before performance measurement. The search function is called in a loop (without inlining), different input array and key from the pre-generated sets are chosen on each iteration. The cumulative sum of all the answers is printed to console to make sure nothing is thrown away by optimizer. Here is the main loop:
int start = clock();
int check = 0;
static const int TRIES = (1<<30) / SIZE;
for (int t = 0; t < TRIES; t++) {
int i = (t * DARR + (MEASURE_LATENCY ? check&1 : 0));
int j = (t * DKEY + (MEASURE_LATENCY ? check&1 : 0));
i &= (ARR_SAMPLES - 1);
j &= (KEY_SAMPLES - 1);
const int *arr = input[i];
int key = keys[j];
int res = search_function(arr, n, key);
check += res;
}
double elapsed = double(clock() - start) / CLOCKS_PER_SEC;
printf("%8.1lf ns : %40s (%d)\n", 1e+9 * elapsed / TRIES, search_name, check);
Originally I wanted to measure only throughput performance, but after having compared the results of MSVC and GCC compilers I realized that I need a mode to measure latency performance too, which is achieved by making input array and key indices dependent on the result of the previous search. The constants ARR_SAMPLES and KEY_SAMPLES are chosen in such a way that the total size of all pre-generated input arrays is equal to the total size of all pre-generated search keys.
There are several reasons for using such a testing environment. First of all, I don't want to include random number generation into performance measurement, that's why input data is generated beforehand. Secondly, I want to avoid branch predictor memorizing the course of execution completely, that's why there are many input arrays and many keys, which are rotated in the loop. It is important that the number of pre-generated keys is large enough. Lastly, I want to be able to emulate reading from prescribed cache level (L1D, L2), and this is approximated by setting the total size of all pre-generated input data appropriately. Unless said otherwise, all the results and plots are given for the fastest L1D cache: input data takes 64 KB of memory, of which input arrays take 32 KB and fit into cache precisely.
All the measurements were done on Intel Core i3-5005U CPU (Broadwell, 2 GHz, no turbo boost). The code was compiled using VC++2017 x64 compiler with /O2 and /arch:AVX2 (unless noted otherwise). For all the plots below, the points on plot lines for binary search implementations have cross-like style, while the points for linear search implementations are marked with bold filled shapes. The plot lines are also grouped by color into: black = branching binary search, blue = branchless binary search, yellow = linear search with break, red/magenta = counting linear search (SSE/AVX).
Here are the names of search implementations:
binary_search_std: direct call to std::lower_boundbinary_search_simple: basic binary search with branchesbinary_search_branchless: branchless binary searchbinary_search_branchless_UR: branchless binary search - fully unrolledlinearX_search_sse: linear search with break (SSE)linear_search_sse: counting linear search (SSE)linear_search_sse_UR: counting linear search (SSE) - fully unrolledlinear_search_avx: counting linear search (AVX)linear_search_avx_UR: counting linear search (AVX) - fully unrolled
Initial attempt
Here is the plot I got initially with results of throughput performance measurement:
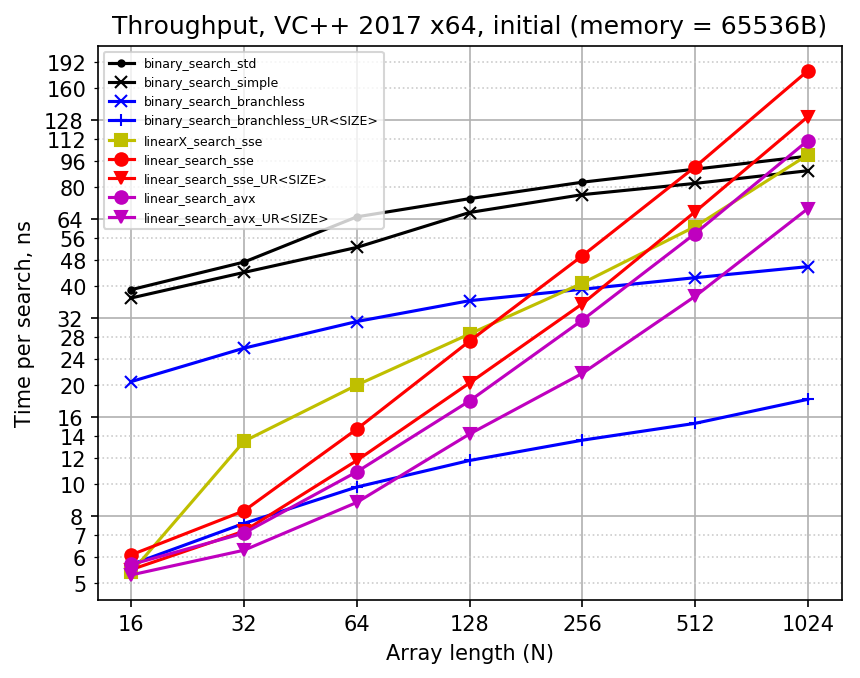
I spent considerable effort analyzing this plot and making conclusions out of it. I wrote a page of text about it =) Of course, I did notice how much performance differs for unrolled and looped versions of branchless binary search. But after looking into assembly output, I did not try to further investigate it. And then I tried to compile the code with GCC (just in case), which changed everything...
With TDM GCC 5.1 x64, I got significantly different throughput performance for several search implementations. Linear searches work more or less in the same time (GCC being slightly slower), but the binary searches are tremendously different:
binary_search_stdimproved from 60 ns to 47 nsbinary_search_simpleimproved from 49 ns to 16 nsbinary_search_branchlessimproved 25 ns to 11 nsbinary_search_branchless_URworsened from 8 to 26 ns
The point 1 is explained by different implementations of STL. The points 2 and 4 are caused by differences in cmovXX instructions generation: binary_search_simple uses cmov on GCC instead of branches (quite unexpectedly: branches were intended), and the assembly code of binary_search_branchless_UR is some terrible mess on GCC, including both cmov-s and branches mixed (that's really bad of GCC). The point 3 cannot be explained so easily: assembly outputs are very similar, and cmov-s are used in both of them.
After having spent some time on blending one assembly code into the other one, I found the critical instruction which spoils everything for MSVC-generated assembly code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | |
The instruction "or r9, -1" on 4-th line is a cunning way of putting -1 into register: it takes only 4 bytes of machine code, while the obvious "mov r9, -1" takes 7 bytes of machine code. It is very similar to the "xor eax, eax" hack for zeroing a register, which every CPU understands today and handles during register renaming. Unfortunately, there is no special handling of instruction "or r9, -1" in Broadwell or other x86 architectures, so false dependency is created: CPU assumes that the new value of r9 register depends on its previous value, which is not set before that in the function. Since the function is called over and over again, most likely the previous value is assigned in line 17 of the previous function call, and it is set to the answer of search. As a result, CPU cannot start executing the next search without knowing the result of the previous one, hence latency is actually measured on MSVC instead of throughput.
This explains why MSVC version is so much slower than that of GCC. If we look into latency measurements (provided below), we'll see the values for binary_search_branchless there equal to those on the plot above.
The issue can be circumvented by assigning value -1 from non-const global variable, then MSVC has to load it from memory (hopefully from L1D) with mov instruction:
intptr_t MINUS_ONE = -1;
int binary_search_branchless (const int *arr, int n, int key) {
//intptr_t pos = -1; //generates "or r9, -1" on MSVC -- false dependency harms throughput
intptr_t pos = MINUS_ONE; //workaround for MSVC: generates mov without dependency
Revised code
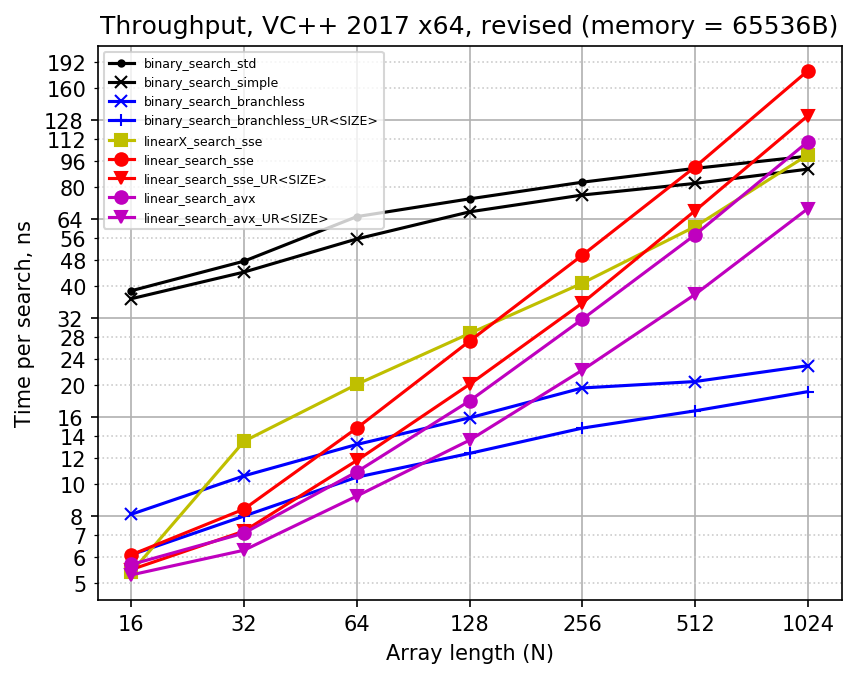
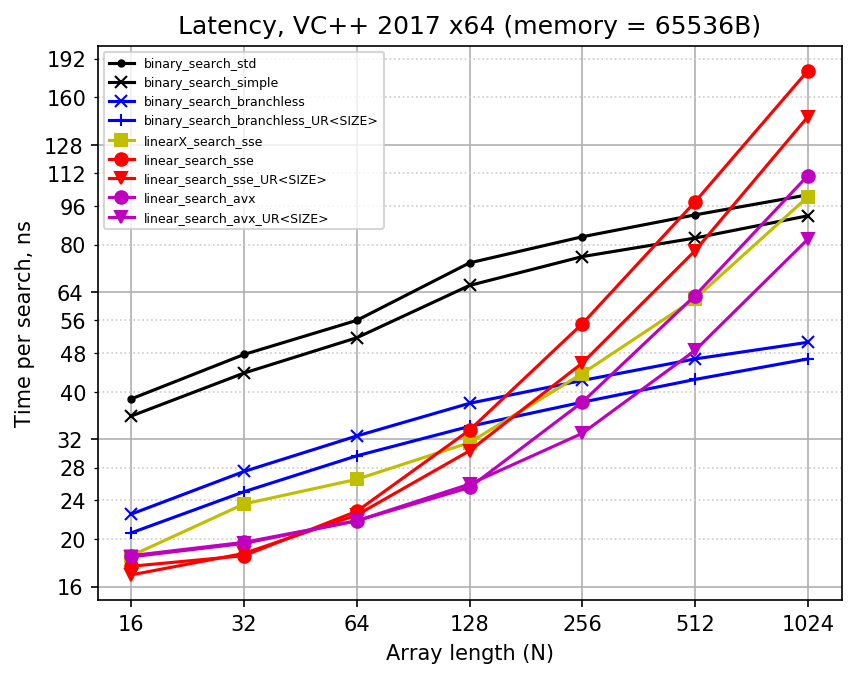
After I resolved the issue with MSVC code gen, I decided that I should measure both throughput and latency time. Here are the results for revised code (throughput and latency performance):
Here are some facts about the results:
- For a binary search, branchless implementation is much faster than branching one: almost four times faster in throughput sense and two times faster by latency. I think it would remain so even if support for non-power-of-two array lengths was added to branchless implementation.
- Full unrolling of branchless binary search (with exactly known number of comparisons to do) makes search faster by about 30% in throughput sense. The difference in latency is negligible: 3-4 cycles.
- It is hard to ensure that binary search written in C++ is branchless on every platform, every compiler and every set of settings. I realized this after looking at GCC's work: it managed to miracously emit cmov in once case and stupidly screw cmov-s in the other place. Also, MSVC screws the last cmov in
binary_search_branchless_URif it is inlined into the benchmark code. There is no way to get cmov-s reliably except for using assembly. - Latency time of branchless binary search is twice as large as throughput time. I suppose it means that CPU runs two searches in parallel when they are independent. However, it can be harder to ensure such independence in real workflow, when binary search is not the only computation done in the hot loop.
- Counting linear search is faster than linear search with break for small N. This is because linear search with break executes unpredictable branch (which does not happen for N = 16 because it always needs one iteration). There is about 60% improvement in throughput for N = 32, and about 35% improvement for N = 64 (less improvement in latency). It seems that the branch costs about 10 cycles in both throughput and latency.
- The linear search with break becomes faster than counting linear search shortly after N = 128. For N = 1024 it is 80% faster, and I guess the performance ratio should converge to two at infinity. This happens because linear search with break processes only half of input array on average, while counting linear search always goes through the whole array. It is questionable whether it is a huge benefit, given that for N > 128 branchless binary search is faster and reads substantially less data anyway.
- For counting linear search, AVX version is noticeably faster only for N = 64, and for larger N it is about 50% faster. Perhaps more efficient AVX implementation would achieve better ratio. As for full unrolling, it gives another almost 50% boost for large N (like N = 256 or more), althrough for small N its benefit is again much less noticeable.
- As for binary vs linear search competition, the situation is different for throughput and latency. For throughput performance, branchless binary search is slower for N < 64 (by at most 30%) and faster for N > 64, although the fully unrolled version of it is as fast as SSE linear search even for N = 16 and N = 32. For latency performance, branchless binary search catches up with SSE linear search only for N between 128 and 256 (double that for AVX), and it is slower by up to 50% for N = 32 and N = 64.
Additional plots
We can also estimate how much time per element is required for each search. Here are the plot where elapsed time is reported per array element (recall that you have to multiply by two to convert from ns to cycles):
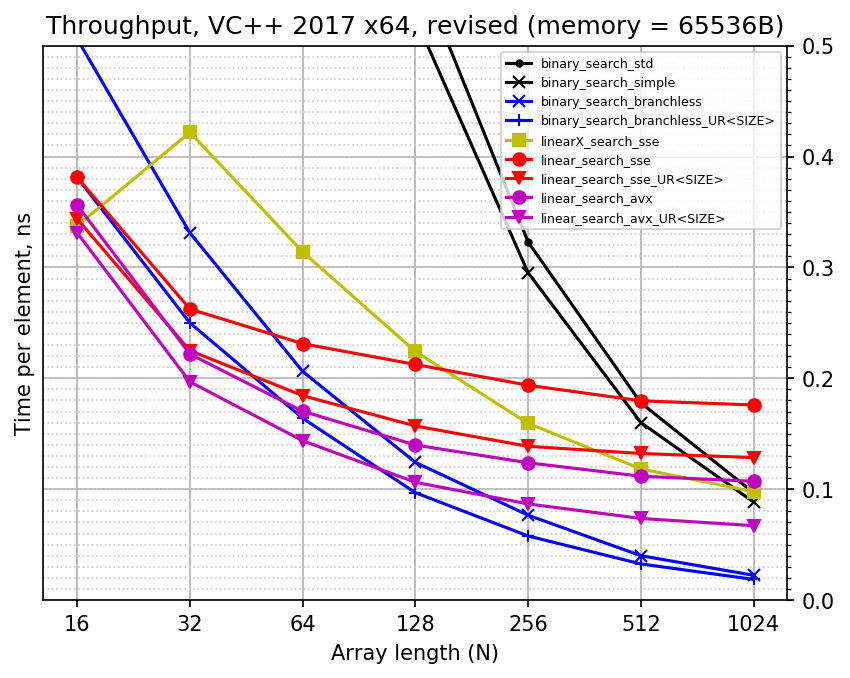
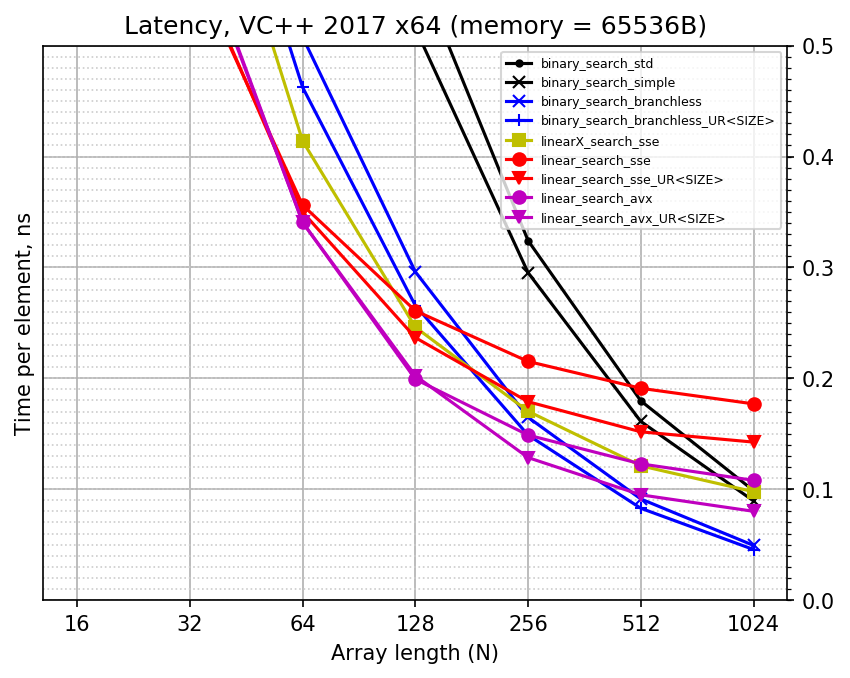
Notice how all the lines are converging to each other on the left: for N = 16 all searches have very similar performance. I think this is the overhead of benchmarking environment which makes them so similar: I simply cannot see e.g. how much faster AVX version is (compared to SSE version) with my crude measuring tool. The linear searches are very compact, for instance unrolled SSE version for N = 16 executes only 16 instructions without any branches at all.
And here is yet another view of the results where time per search is divided by the logarithm of N (i.e. by the number of comparisons in binary search). It shows the constant in O(log N) estimate for binary searches, just like the previous plot shows constant in O(N) estimate for linear searches. These images can be helpful to estimate the cost of single step of a binary search.
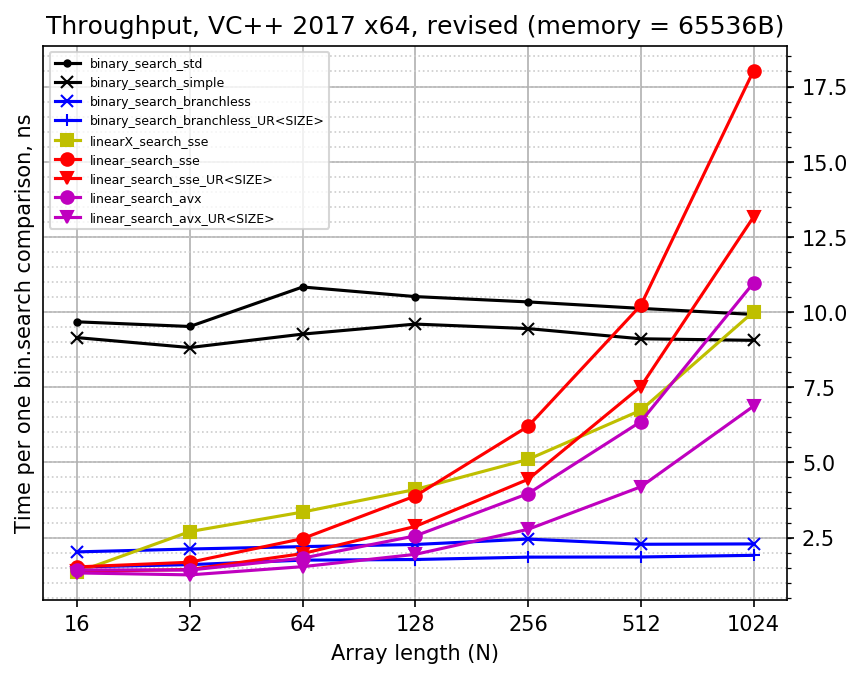
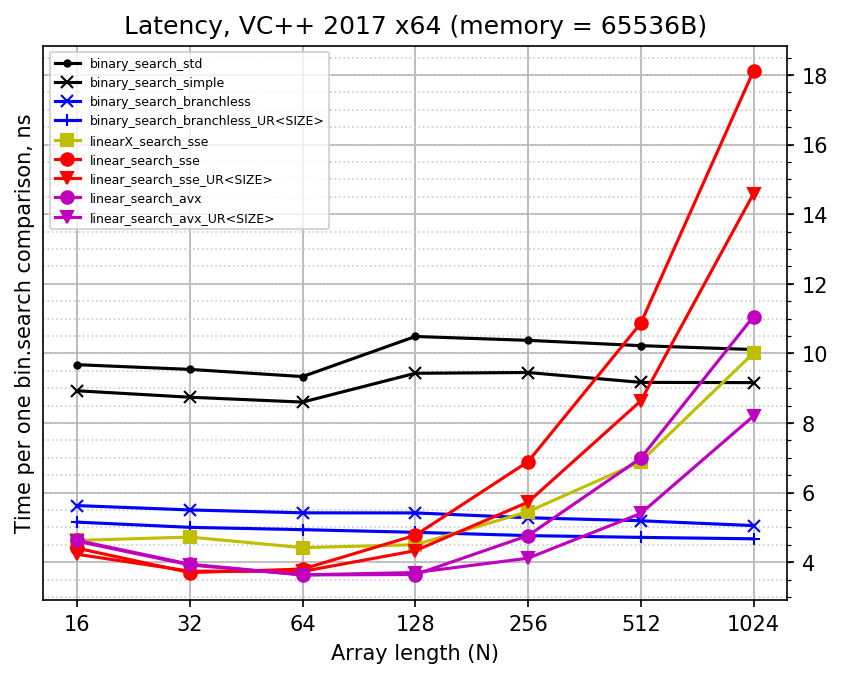
Finally, below are plots recorded while using 512KB of input data, which tries to simulate L2 memory access. The CPU has 256 KB of L2 cache per core, which means that all input arrays fit into it perfectly. It seems that adding L1 cache misses into benchmark makes things closer to each other, but does not change the situation much.
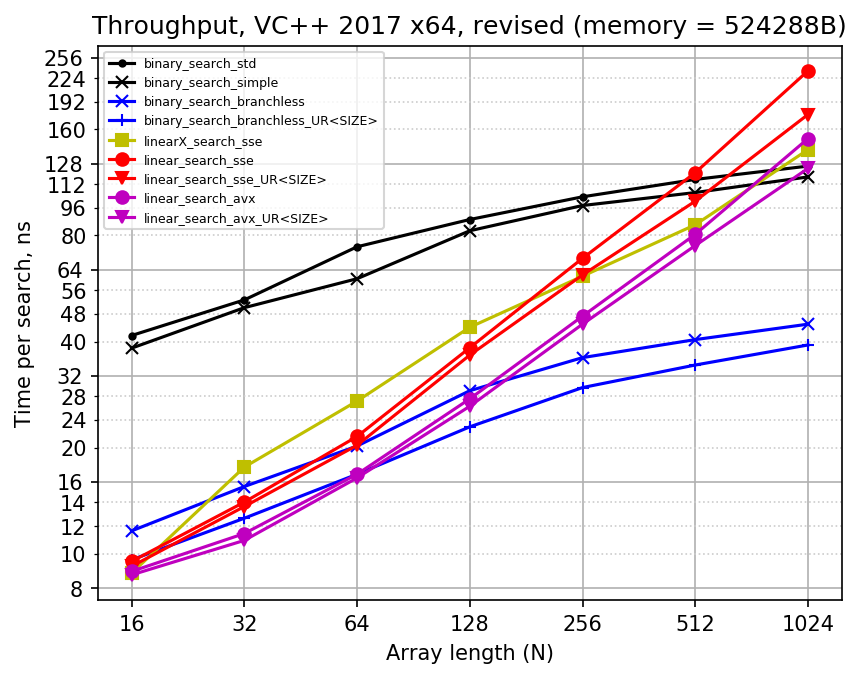
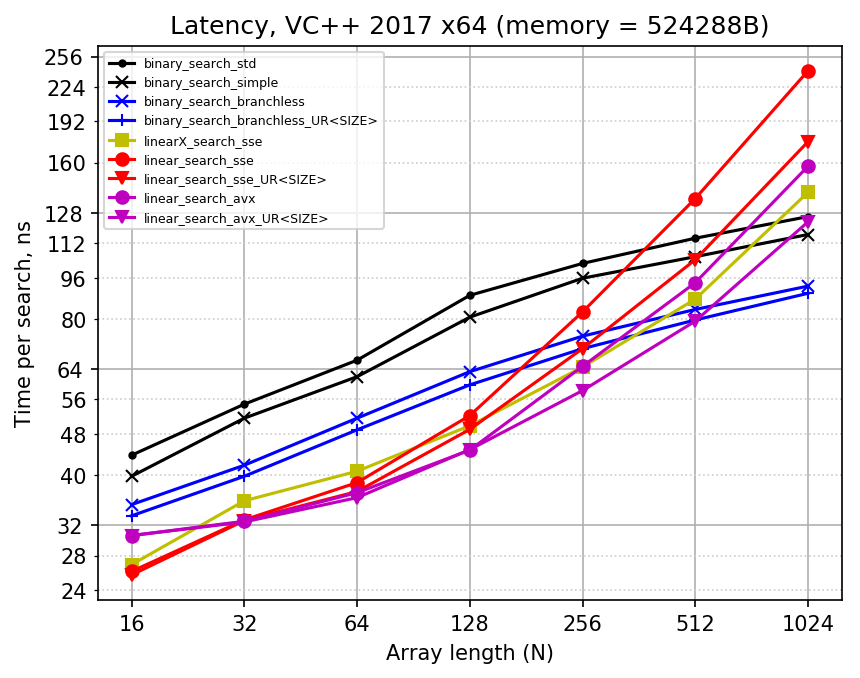
Note that not all memory loads are forced to access L2 cache, sometimes faster L1 cache is also used. If you consider counting linear search, it always accesses all the array elements during search. Because of that the whole 256 KB of input array data is accessed over and over again, which makes sure that it is read from L2 cache. In case of binary search, different elements have different probability of being accessed: for N = 1023, 511-st element is always accessed, elements 255 and 767 are accessed with probability 50%, even-indexed elements have probability 0.2% of being accessed (see more about it in this bannalia blog post) So it is quite likely that the most popular elements get into smaller L1 cache, accelerating several first comparisons in the search. For instance, for N = 512 there are 128 input arrays and 32 KB of L1D cache, so each input array gets 4 cache lines in L1D, enough to accelerate first two iterations. This is a natural benefit of binary search, which works in real world too.
The code
All the code and materials are available in GitHub repository linear-vs-binary-search.
Conclusion
The proposed "counting" linear search is noticeably faster for small array lengths than linear search with break, because branch misprediction is removed from it. So it makes sense to always use counting version of linear search instead of the breaking one, since for larger array lengths binary search becomes faster anyway.
Binary search is surprisingly good to stand against linear search, given that it fully utilizes conditional move instructions instead of branches. In my opinion, there is no reason to prefer linear search over binary search, better make sure that your compiler does not generate branches for the binary search. Counting linear search is worth using only in a rare case when it is known that array length is very small and the search performance is really critically important. Also, the idea of counting linear search is easy to embed into some vectorized computation, unlike the binary search.
Addendum
I decided to keep all the additional information about this article in a separate blog post. You may find more information in the addendum, including some more implementations and extended performance comparison.
This article is discussed on reddit here.