Recently I stumbled upon a question on stackoverflow, which asked how to vectorize computing symmetric difference of two sorted int32 arrays using AVX2. I decided to try doing it myself, and this post is about what I achieved. Of course, the best way to compute symmetric difference of sorted sets is by running ordinary merge algorithm (e.g. with std::merge) for the arrays plus some simple postprocessing. I'll concentrate only on the generic merging algorithm here.

I'll handle 32-bit integer keys only. Having keys of larger size would reduce significantly the efficiency of the algorithm (as usual with vectorization). Using 32-bit floating point keys is not much different from using integer keys; moreover, sorting 32-bit floats can be easily reduced to sorting 32-bit integers, which is often used to run radix sort on floating point data (see this and that). Also I'll briefly discuss the case when 32-bit values are attached to 32-bit keys (sorting without values is pretty useless in practice).

Better scalar code

Before trying to vectorize the algorithm, let's try to see how fast scalar implementation can be. Here is a simple implementation of merging algorithm:

int Merge_ScalarTrivial(const int *aArr, int aCnt, const int *bArr, int bCnt, int *dst) {
    int i = 0, j = 0, k = 0;
    while (i < aCnt && j < bCnt) {
        if (aArr[i] < bArr[j])
            dst[k++] = aArr[i++];
        else
            dst[k++] = bArr[j++];
    }

    memcpy(dst + k, aArr + i, (aCnt - i) * sizeof(dst[0]));
    k += (aCnt - i);
    memcpy(dst + k, bArr + j, (bCnt - j) * sizeof(dst[0]));
    k += (bCnt - j);
    return k;
}

The first possible improvement is about termination criterion. Since the inner loop is tiny, checking i < aCnt and j < bCnt can take noticeable time (note also that both i and j grow unpredictably). This can be improved in one of three ways:

1. Add sentinel element (INT_MAX) immediately after each input array, so that we can iterate by k in range [0 .. aCnt + bCnt). This approach is great, and the main drawback is that it forces us to copy the whole input if we cannot freely overwrite such after-the-end elements.
2. Do iterations in blocks of size 32 (for instance). Just replace the condition of while with i <= aCnt - 32 && j <= bCnt - 32, and add second loop for (int t = 0; t < 32; t++) just inside the first one. This way the innermost loop has simple stop criterion t < 32, and the outer loop terminates when it cannot be guaranteed that the inner loop won't get out of any input array. The remaining iterations are processed in the usual way, which is not very nice of course (there can be many iterations remaining).
3. (taken). Carefully detect when exactly the loop finishes. In order to achieve this: find which input array has greater last element, then iterate back from that element to detect all elements which get into memcpy-ed tail. Given that number of such elements is X, we can freely replace the loop with for (int k = 0; k < aCnt + bCnt - X;). In future with vectorization, we'll have to generalize this approach so that at least four elements are always available in the inner loop: this is achieved by doing merge in reversed order (from the ends of both arrays) until both arrays have at least four elements processed.

The second improvement is removal of branch if (aArr[i] < bArr[j]). This branch is completely unpredictable if the input arrays are randomly interleaved, which makes CPU do excessive work and increases latency of each iteration. In order to determine which element must be stored into dst[k], it is enough to use ternary operator, which would compile into cmov instruction. In order to increment i and j counters, we can add boolean results of some comparisons to both of them, which would compile into setXX instructions.

These two changes reduce average time per element from 6.5 ns to 4.75 ns (on random inputs, on my laptop). Here is the resulting code:

int Merge_ScalarBranchless_3(const int *aArr, int aCnt, const int *bArr, int bCnt, int *dst) {
    //let's assume values = INT_MIN are forbidden
    int lastA = (aCnt > 0 ? aArr[aCnt-1] : INT_MIN);
    int lastB = (bCnt > 0 ? bArr[bCnt-1] : INT_MIN);
    if (lastA < lastB) //ensure that lastA >= lastB
        return Merge_ScalarBranchless_3(bArr, bCnt, aArr, aCnt, dst);
    int aCap = aCnt;
    while (aCap > 0 && aArr[aCap-1] >= lastB)
        aCap--;

    size_t i = 0, j = 0, k = 0;
    for (; k < aCap + bCnt; k++) {
        int aX = aArr[i], bX = bArr[j];
        dst[k] = (aX < bX ? aX : bX); //cmov
        i += (aX < bX);               //setXX
        j += 1 - (aX < bX);           //setXX
    }
    assert(i == aCnt || j == bCnt);

    memcpy(dst + k, aArr + i, (aCnt - i) * sizeof(dst[0]));
    k += (aCnt - i);
    memcpy(dst + k, bArr + j, (bCnt - j) * sizeof(dst[0]));
    k += (bCnt - j);
    return k;
}

Idea of vectorization

The main problem with the merge algorithm is that it is inherently sequental. Before you finish comparison of two head elements, you cannot compare the next ones, you don't even know which two elements you have to compare next. This issue makes both scalar and vectorized code run slower, because instructions have to wait for each other to complete, and the compute units in CPU stay idle during this time.

Another problem is that the data is moved and shuffled in complex and dynamic ways during merging process. This is not noticeable in scalar implementation, because you operate on only two elements at a time. But if you want to vectorize merge operation, you have to work with more elements at once. If you take four elements from each array, you soon realize that these elements must be shuffled in one of 70 ways to get them into single sorted sequence. This is a big issue for vectorization, because it was mostly designed to do some simple r[i] = a[i] + b[i] things:

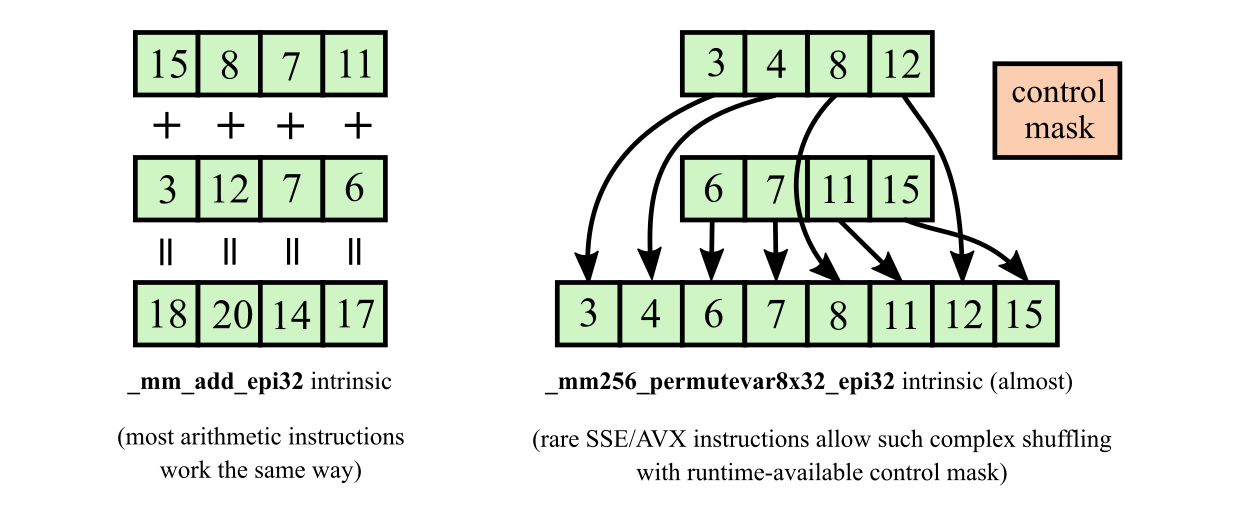
Yes, SSE and AVX have many shuffling operations. But most of them accept only immediate operand (i.e. compile-time constant) as control mask, so they can only shuffle data in a static way. The rare exceptions are: pshufb (_mm_shuffle_epi8) from SSSE3, vpermilpd and vpermilps (_mm256_permutevar_p?) from AVX, and vpermd and vpermps (_mm256_permutevar8x32_*) from AVX2. The first two can only shuffle data within 128-bit blocks, but the last one can shuffle eight 32-bit integers within 256-bit register in arbitrary way, which should allow us to merge 4 + 4 elements in one iteration.

Constructing shuffle control mask directly in the code is possible, but this is often too complex, and thus too slow. This is where lookup table (LUT) comes into play. The generic approach looks like this:

1. Obtain enough information about input (f.i. by comparing elements), so that the needed shuffle control mask could be uniquely determined from this information.
2. Convert information into compact bitmask in general purpose register (usually done by some shuffling and movemask intrinsic).
3. (optional) Apply perfect hash function (e.g. some multiplicative hash) to bitmask to obtain number of smaller size.
4. Use obtained number as index in a lookup table. The corresponding element of the table must contain the desired control mask for shuffling (precomputed beforehand).

If this sounds complicated, just wait a bit: in the next section all of these steps will be thoroughly explained on example.

Speaking of our particular merging problem, we will use this approach to process four input elements per iteration. Suppose that from each input array, four minimal elements are loaded into xmm register. First of all, we merge these eight elements into a single sorted sequence. First half of the resulting sequence (4 elements) can be stored to the destination array immediately. The second half should remain in processing, because some future input elements can still be less than them.

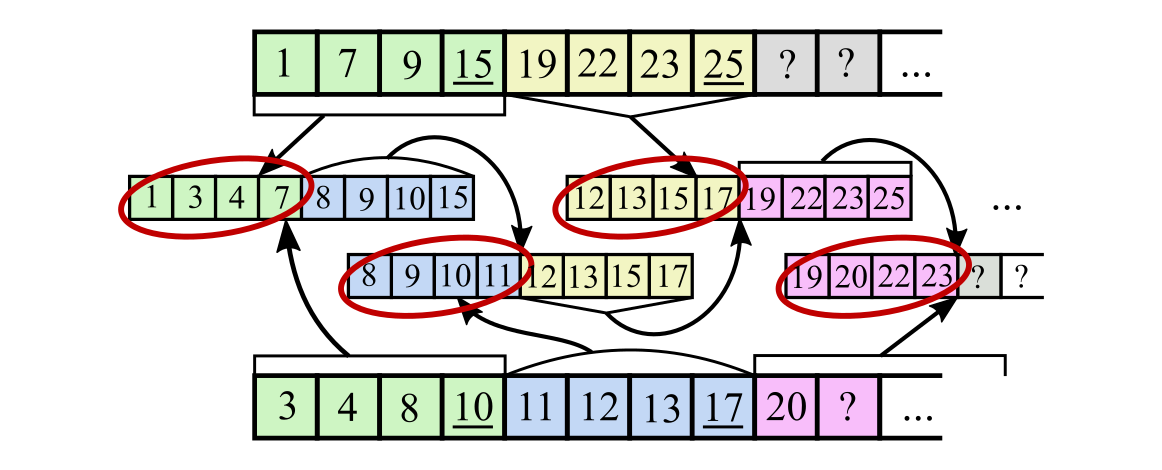
An important question here is: how to move pointers in the input arrays? What are we going to load and process on the next iteration? Two approaches come into mind (see pictures below):

1. Move each input pointer by number of its elements written to destination array (i.e. by how many elements from input array got into the four minimal elements of the sorted eight-element sequence). It means one of: move each pointer by two elements, move only one pointer by four elements, or move one pointer by three and the other pointer by one. On the next iteration, we'll simply load four elements again from each array using corresponding moved pointer. This approach has many drawbacks: we have to use unaligned loads for input arrays, we have to load each input element twice on average, and we have to spend additional time on computing the pointer movements. Moreover, it is hard to learn what exactly we must load for the next iteration until we have fully sorted the eight elements on the current iteration: this makes dependency chain quite long. Here is an illustration:

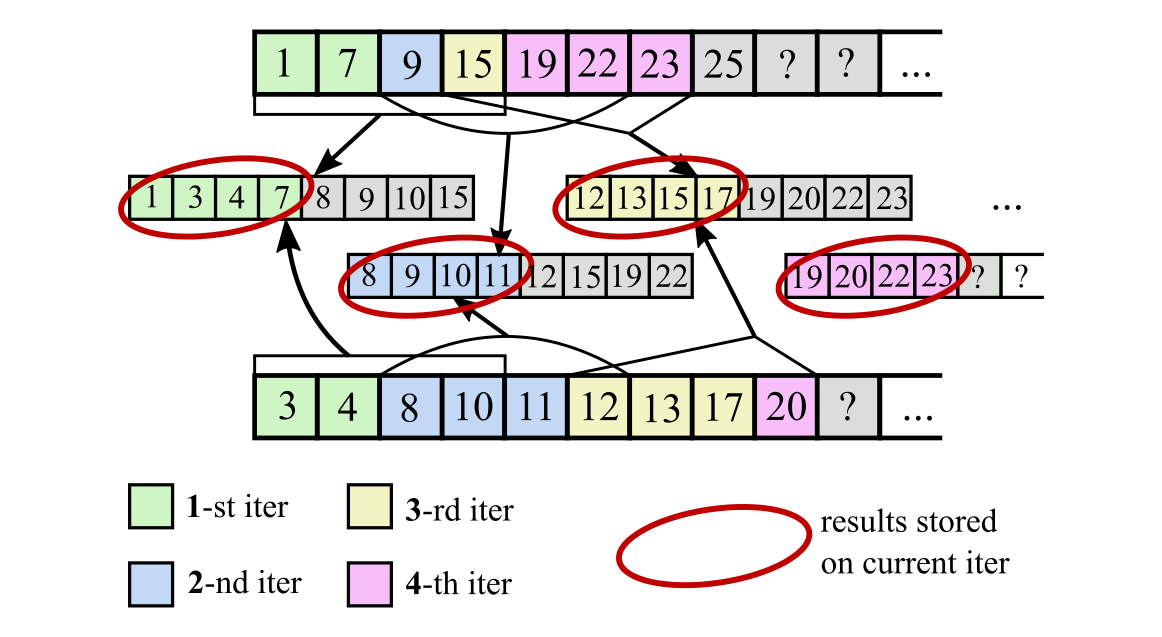
2. (taken). Move one input pointer by exactly four elements, leave the other one unchanged. When choosing which pointer to move, look where the last element considered is less: it should be moved. Let it be e.g. from the input array B; then on the next iteration the next four elements from B must be loaded and processed. We cannot use the same four elements from A on the next iteration, because some of them may already be dumped to the destination array. So we take the second half of the sorted eight-element sequence from the current iteration to be used as four elements from A on the next iteration (these are exactly the elements loaded from A and B which are not yet dumped to the destination array). The core advantage here is that we can determine which pointer to move without waiting for the eight-element sorted sequence to be computed. It means that CPU will load the data for the next iteration and compare/sort the current data in parallel.

Implementation

Assume for simplicity that all input elements are distinct: then there is unique order in which the elements must go in the merged sequence. Let's suppose that we already have four elements from A loaded into srcA, and four elements of B loaded into srcB (both are xmm registers).

Here is an illustration for steps 1-4 and step A:

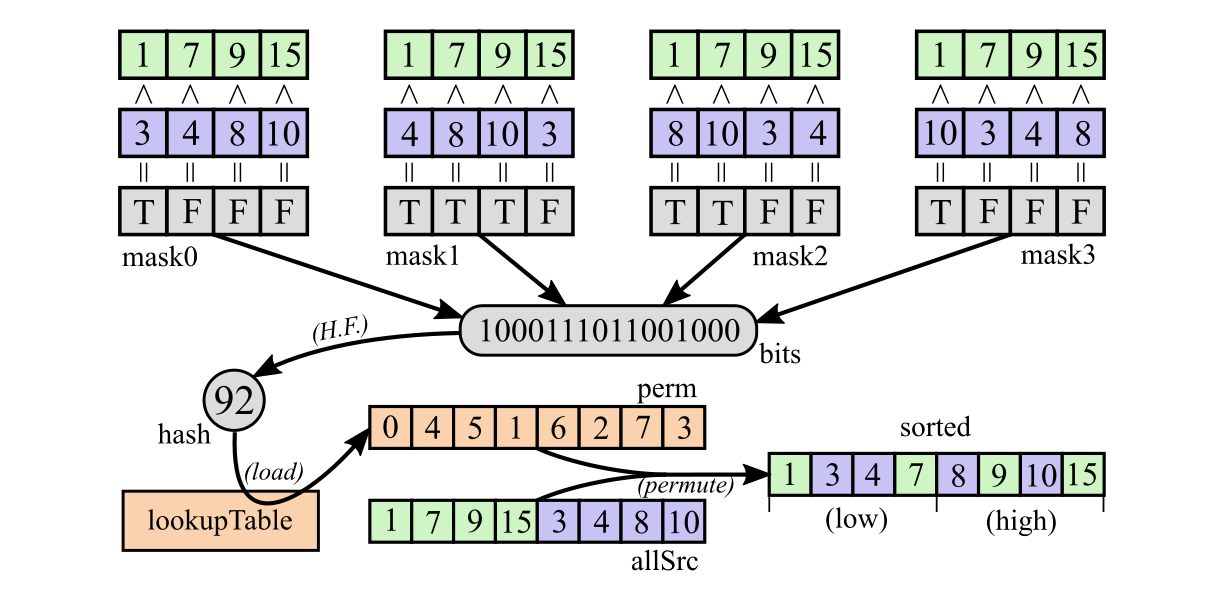
Step 1. It is enough to compare all elements from srcA with all elements from srcB to fully determine their order in the common sorted sequence. In fact, the position of element srcA[i] in the final sorted array is equal to number of elements from srcB less than it plus its index i. If AVX2 had shuffling instruction which accepts scatter-style indices, we could even construct shuffle control mask directly without LUT using this property =) Unfortunately, SSE/AVX shuffles accept only gather-style indices.

This means we need to perform 16 comparisons (4 x 4) in total. Clearly, we can do four comparisons in single instruction, then rotate one of the registers by one element and compare again, and then repeat it two more times --- as the result, we'll get four xmm registers with comparison results bitmasks.

[1]  __m128i mask0 = _mm_cmplt_epi32(srcA, srcB);
[2]  __m128i mask1 = _mm_cmplt_epi32(srcA, _mm_shuffle_epi32(srcB, SHUF(1, 2, 3, 0)));
[3]  __m128i mask2 = _mm_cmplt_epi32(srcA, _mm_shuffle_epi32(srcB, SHUF(2, 3, 0, 1)));
[4]  __m128i mask3 = _mm_cmplt_epi32(srcA, _mm_shuffle_epi32(srcB, SHUF(3, 0, 1, 2)));

Step 2. Sixteen comparisons means that we should be able to get 16-bit mask, where each bit corresponds to the result of single comparison. In order to achieve this, we pack all the four bitmasks obtained on the previous step into single xmm register, where each byte contains result of one comparison. Using intrinsic _mm_packs_epi16 three times does this exactly. Then apply _mm_movemask_epi8 to the result: it gets sign bits of all 16 bytes and puts them into single 16-bit mask in general purpose register.

[5]  __m128i mask01 = _mm_packs_epi16(mask0, mask1);
[6]  __m128i mask23 = _mm_packs_epi16(mask2, mask3);
[7]  __m128i mask = _mm_packs_epi16(mask01, mask23);
[8]  uint32_t bits = _mm_movemask_epi8(mask);

Step 3. The obtained 16-bit bitmask can be used directly to load control mask from a lookup table. However, such a lookup table would take 65536 x 32 B = 2 MB of space, and the algorithm would read randomly some of its entries. This would waste precious TLB entries, so it would be great to compress this LUT somehow.

First we need to understand how many entries are really used in the table. Notice that each 16-bit mask determines precisely the ordering of all eight elements and vice versa (recall: all elements are distinct for now). Given that each set of four elements is sorted, each global ordering corresponds to a coloring of eight things into black and white, so that four things are colored in each color. This is binomial coefficient C(8,4) = 70. So only 70 bitmasks of 65536 are really possible as values of bits variable.

Now we want to create a hash function which maps valid bitmasks into integers from 0 to K-1, so that K is quite small (a bit greater than 70), hash function is perfect (i.e. gives no collisions) and blazingly fast to compute. Multiplicative hash function fits well under these criteria:

$f(x) = \left\lceil \frac{A \cdot x}{2^{32-b}} \right\rceil;$ where $x \in [0 \ldots 2^{32}), A \in (0 \ldots 2^{32}), b \in [0 \ldots 32)$.

For the problem considered, there is such a hash function for b = 7 and A = 0x256150A9. The code for its usage is:

[9]   uint32_t hash = ((bits * 0x256150A9U) >> 25);
[10]  __m256i perm = ((__m256i*)lookupTable)[hash];

This also finishes step 4 from the generic description above.

LUT generation. This part can easily take more time and more code than the whole merging algorithm =) But in its essence, it is just a small exercise in algorithmic programming. I'll only outline how it is done, you can look at the full code at the end of the article if you want.

1. Iterate through all 8-bit bitmasks with exactly 4 bits set: the i-th bit says from which input array i-th element in the sorted sequence comes (in fact this is an even coloring of eight elements into two colors). For each of them:
   1. Assign numbers e.g. from 0 to 7 to the elements, so that they go in proper order according to the coloring. Note that exact values of the elements do not matter, only their ordering does.
   2. Generate 16-bit bitmask by doing all pairwise comparisons between the elements from each input array exactly as you do it in the merging algorithm (4 x 4 comparisons, one bit generated by each of them). This is the key for LUT.
   3. Generate the desired shuffle control mask which you need to use in this exact case to get the sorted sequence. This is the value for LUT.
   4. Dump all 70 key-value pairs into an array.
2. Generate perfect hash function of the form shown above for the keys. For a fixed value of b (for instance, b = 7), iterate over all values of A. For each value, apply hash function to all the 70 keys and check for collisions. If there are no collisions, then you are done; otherwise, try the next value of A. This step took about a minute of computing time on my laptop.
3. Apply the generated hash function to each key, and save corresponding value into the entry of lookup table with the obtained index.
4. Dump the obtained lookup table into a text file in C++-compilable format. Then copy/paste its contents into your C++ file, so that you don't have to generate this data each time during program startup.

Step A. Now we have to apply this magic shuffling intrinsic _mm256_permutevar8x32_epi32. Since we have input elements in two separate xmm registers, we have to combine them first. Also, we have to split the result into two halves afterwards.

[11]  __m256i allSrc = _mm256_setr_m128i(srcA, srcB);
[12]  __m256i sorted = _mm256_permutevar8x32_epi32(allSrc, perm);
[13]  __m128i sortedLow = _mm256_castsi256_si128(sorted);  //nop
[14]  __m128i sortedHigh = _mm256_extractf128_si256(sorted, 1);

Note that the elements from the lower half can be stored immediately into the destination array:

[15]  _mm_store_si128((__m128i*)(dst + k), sortedLow);
[16]  k += 4;

Step B. Finally, we have to move the pointers in the input arrays. More precisely, we want to move only one pointer by 4 elements, depending on how the last elements in srcA and srcB compare to each other. We want to avoid branches (not to waste CPU time) and memory accesses (to keep latency low).

I must admit that there are a lot of ways to achieve it, and tons of possible code snippets that do it. Moreover, each snippet may compile to different assembly code, depending on exact choice of intrinsics and bitness/signedness of integer variables. I'll just describe the approach which worked best for me among numerous tries I did.

There are two pointers ptrA and ptrB: each of them moves along one of the input arrays. To simplify code, we want to sometimes swap these two pointers, so that one specific pointer (e.g. ptrB) is always moved. Unfortunately, it is quite hard to efficiently swap two registers on condition in branchless fashion, but it becomes easier if we maintain address difference abDiff = ptrB - ptrA instead of the pointer ptrB. In such case swapping is equivalent to ptrA = ptrA + abDiff and abDiff = -abDiff.

First of all, recall that we have already compared 3-rd elements of srcA and srcB, and the result is saved in mask0 register. Let's extract it from there into GP register:

[17]  __m128i mask0last = _mm_shuffle_epi32(mask0, SHUF(3, 3, 3, 3));
[18]  size_t srcAless = _mm_cvtsi128_sz(mask0last);

_mm_cvtsi128_sz is a macro for _mm_cvtsi128_si32 or _mm_cvtsi128_si64, depending on bitness.

Then we want to swap pointers if srcAless = -1, and retain their values if srcAless = 0. The following ugly piece of code achieves that in 4 instructions:

[19]  aPtr = (const int *)(size_t(aPtr) + (abDiff & srcAless));
[20]  abDiff ^= srcAless;  abDiff -= srcAless;

Now the 3-rd element from ptrA is surely greater, so we have to move the ptrB pointer. Since we do not maintain ptrB, we have to increase abDiff instead:

[21]  abDiff += 4 * sizeof(int);

After that we load four new elements from ptrB (do not forget that the pointer must be computed):

[22]  bPtr = (const int *)(size_t(aPtr) + abDiff);
[23]  srcB = _mm_load_si128((__m128i*)bPtr);

According to the plan (see above), we must use higher half of the sorted sequence in place of the elements from array A on the next step, so:

[24]  srcA = sortedHigh;

The description of the vectorized implementation ends here.

Full code. All the code snippets gathered above can be combined to get a working merge function:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

int Merge_Simd_KeysOnly(const int *aArr, int aCnt, const int *bArr, int bCnt, int *dst) {
    //merge input arrays in reverse direction (from ends)
    intptr_t i = aCnt - 1, j = bCnt - 1, k = aCnt + bCnt - 1;
    while (i >= 0 && j >= 0 && (i >= aCnt - 8 || j >= bCnt - 8)) {
        if (aArr[i] < bArr[j])
            dst[k--] = bArr[j--];
        else
            dst[k--] = aArr[i--];
        //TODO: any vectorized code if loop does not finish soon?
    }
    i++, j++, k++;

    //these cases are necessary to ensure that arrays are long enough
    if (i == 0) {
        memcpy(dst, bArr, j * sizeof(dst[0]));
        return aCnt + bCnt;
    }
    if (j == 0) {
        memcpy(dst, aArr, i * sizeof(dst[0]));
        return aCnt + bCnt;
    }

    //prepare for the first iteration
    size_t maxK = k, tail = aCnt + bCnt - k;
    const int *aPtr = aArr;
    const int *bPtr = bArr;
    intptr_t abDiff = intptr_t(bArr) - intptr_t(aArr);
    __m128i srcA = _mm_load_si128((__m128i*)aPtr);
    __m128i srcB = _mm_load_si128((__m128i*)bPtr);

    for (k = 0; k < maxK; ) {
        //inner-loop: combined from all the snippets
        __m128i mask0 = _mm_cmplt_epi32(srcA, srcB);
        __m128i mask1 = _mm_cmplt_epi32(srcA, _mm_shuffle_epi32(srcB, SHUF(1, 2, 3, 0)));
        __m128i mask2 = _mm_cmplt_epi32(srcA, _mm_shuffle_epi32(srcB, SHUF(2, 3, 0, 1)));
        __m128i mask3 = _mm_cmplt_epi32(srcA, _mm_shuffle_epi32(srcB, SHUF(3, 0, 1, 2)));
        __m128i mask = _mm_packs_epi16(_mm_packs_epi16(mask0, mask1), _mm_packs_epi16(mask2, mask3));
        uint32_t bits = _mm_movemask_epi8(mask);

        uint32_t hash = ((bits * 0x256150A9U) >> 25);
        __m256i perm = ((__m256i*)lookupTable)[hash];

        __m256i allSrc = _mm256_setr_m128i(srcA, srcB);
        __m256i sorted = _mm256_permutevar8x32_epi32(allSrc, perm);
        __m128i sortedLow = _mm256_castsi256_si128(sorted);
        __m128i sortedHigh = _mm256_extractf128_si256(sorted, 1);

        size_t srcAless = _mm_cvtsi128_sz(_mm_shuffle_epi32(mask0, SHUF(3, 3, 3, 3)));
        //conditionally swap ptrA and ptrB (abDiff)
        aPtr = (const int *)(size_t(aPtr) + (abDiff & srcAless));
        abDiff ^= srcAless;  abDiff -= srcAless;

        abDiff += 4 * sizeof(int);
        bPtr = (const int *)(size_t(aPtr) + abDiff);
        srcA = sortedHigh;
        srcB = _mm_load_si128((__m128i*)bPtr);

        _mm_store_si128((__m128i*)(dst + k), sortedLow);
        k += 4;
    }
    return aCnt + bCnt;
}

Generality

Equal elements

The algorithm (and the code) works properly even if equal elements are present. It can be checked using the "perturbation method", which is sometimes used to resolve singular cases in computational geometry.

Imagine that eps is a small positive number much less than 1. Consider packs srcA and srcB with four integers in each. Add i*eps to srcA[i] and subtract j*eps from srcB[j]. This perturbation does not change the masks generated during step 1 of the algorithm, because we do only comparisons of style "A[i] < B[j]" there. The code works properly for perturbed elements (because they are distinct), and it will shuffle the original elements in exactly the same way, so after step 4 we'll get properly sorted eight-element sequence.

The last thing to note is that when we choose which pointer to move, we can choose any of the two if their last elements are equal (just as we do in the ordinary scalar merge if elements are equal).

Key-value pairs

It is rather easy to extend the code to work with 32-bit values attached to 32-bit keys. The idea is to store four values in register valuesA for the four keys stored in register srcA, and do the same for array B. All the data movement happening on the keys must be exactly reproduced on the values too.

The lines 1-10 of the code listing are only gathering information about keys, so they can be left untouched. The lines 11-14 must be duplicated for the values with the same shuffle control mask.

If keys and values are provided in separate arrays (SoA layout), then lines 19-22 must also be duplicated, since values would have their own pointer into array A and difference between pointer addresses. And this is rather unfortunate, because it is a lot of instructions. On the other hand, lines 15 and 23 (load/store) can be simply duplicated without any changes.

If keys and values are interleaved (AoS layout), then it becomes a bit simpler. Lines 11-14 can be left untouched, but loads and stores in lines 15 and 23 must be accompanied with some shuffling to interleave/deinterleave keys and values (in addition to duplication, of course).

Performance

For testing performance, two integer sequences of length N were generated, each element is random with uniform distribution from 0 to 3*N. After that both of the sequences were sorted. Then all the methods were run on these two input arrays, each method was run many times in a row. Note that each run was done on the same input, and it is very important especially for small N, where branch predictor can simply memorize everything. Total elapsed time was measured, and average time in nanoseconds per one output element was computed. This time is shown in this table: 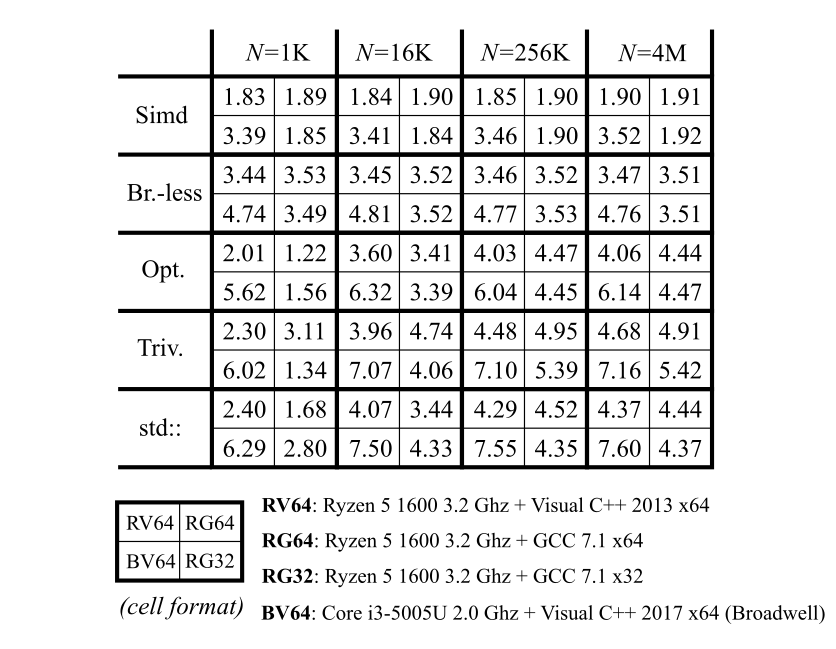Five implementations were tested:

• Simd: vectorized version based on SSE/AVX2 (Merge_Simd_KeysOnly function described in the article)
• Br.-less: scalar version without branches (see Merge_ScalarBranchless_3 function listing)
• Opt.: optimized scalar version with branches (not shown in the article)
• Triv.: baseline scalar version with branches (see Merge_ScalarTrivial function listing)
• std::: direct call to std::merge (scalar, with branches)

Note that only the first two implementations were thoroughly optimized. That's why e.g. "Triv." performance is so different on 32-bit vs 64-bit. Most likely I did not inspect the assembly output, so there are some excessive 32/64-bit conversions, which normally does not affect performance, but in such tiny loops it becomes very important.

Although results for N = 1K are provided, they have little sense actually. I'm pretty sure that branch predictor simply memorized how the elements compare to each other, that's why scalar implementations with branches become so fast. In the real world, the input sequences would be different each time, so the performance results would be different too.

I was testing GCC in VirtualBox VM, and I hope that it does not affect the results too much. Speaking of MSVC vs GCC comparison, the first two implementations work equally well on them.

Brand new AMD Ryzen CPU and mobile Intel CPU (broadwell) were used for performance measurements. The two main implementations are branchless, and they work almost the same way on both processors. The one really interesting thing here is that the solutions with branches for N = 1K work a lot better on Ryzen then on Broadwell. I suppose the well-marketed branch predictor based on neural net does its job well and memorizes all the branches, unlike its Intel counterpart =)

All the code is available in this gist (both merge implementations and lookup table generator).

Conclusion

The vectorized version is 1.8 times faster than the scalar branchless version, and 2.3 times faster than std::merge. Is such a speedup worth all the trouble?! I think not =)

A related but simpler problem is set intersection problem: find all common elements in two strictly increasing arrays. A vectorized solution for it (very similar to the algorithm described in this article) is described in this blog post, and its optimized version is available here.

You might ask: why is the performance improvement from vectorization so low? is it because of lookup table or something else? I think I'll save these questions for another post =) Aside from some analysis of the code shown here, I'll try to implement merge sort on top of it. I wonder if I could beat std::sort with it...