The previous blog post got some attention and several good questions and suggestions. So I feel that I should sum up the main points noted by readers. Since the main article is already too long, I decided to keep all of this as a separate post.

Large arrays

Let's make it clear: the whole blog post was only about small arrays!

Since I was interested in linear search more than in binary search, I was mainly interested in cases like N <= 128. It is clear that for larger arrays linear search is out of consideration anyway. All the performance results (except for one pair of plots) were measured in such a way that everything important fits into L1D cache. All the complicated things about memory access like using L2/L3/TLB/RAM were not considered at all. That's why the provided results may mislead if you want to implement binary search over 1 MB array.

Speaking of really large arrays, there are several points to consider:

1. The provided implementation of branchless binary search always has power-of-two step, which causes ill cache utilization for large arrays (due to limited cache associativity). One of the solutions would be using ternary search instead of binary one. You can read more about it in Paul Khuong's blog post.
2. If you can reorder allements beforehand, better rearrange them so that frequently used elements go first. The resulting layout is equivalent to storing perfectly balanced binary search tree in breadth-first order. This order is much more cache-friendly. Read more in bannalia's blog post.
3. If you can rearrange/preprocess large array, probably you should use some data structure for your searches. Various variations of B-tree are the most promising. You can read a bit about it e.g. in this article.

Branchless without ternary operator

Regarding branchless binary search, some wondered if this can really be called branchless:

//binary_search_branchless
pos = (arr[pos + step] < key ? pos + step : pos);

There is no point in arguing about terminology, but it is quite interesting to see how other versions perform. For instance, it is possible to use the result of comparison as 0/1 integer value and do some math on it:

//binary_search_branchlessM
pos += (arr[pos + step] < key) * step;

//binary_search_branchlessA
pos += (-(arr[pos + step] < key)) & step;

Also, it is possible to avoid comparison completely, using arithmetic shift on difference to get empty or full bitmask:

//binary_search_branchlessS
pos += ((arr[pos + step] - key) >> 31) & step;

Just remember that this code is not perfectly portable: it relies on undefined behavior according to C/C++ standards.

I included these three cases into extended comparison (see plots below). They are noticeably slower of course, but still much faster than branching binary search.

Preload pivot elements

One really smart idea about binary search was from seba, who suggested preloading both possible pivots for the next iteration while still performing the current iteration. This means doing two memory loads per iteration instead of one, but since they are started one iteration earlier, their latency is hidden behind other logical instructions going on.

Note that after both potential pivots are loaded, we need to do additional work to choose the real future pivot among them, and it can be done with cmov with after the comparison already performed. Here is the resulting implementation:

int binary_search_branchless_pre (const int *arr, int n, int key) {
    intptr_t pos = MINUS_ONE;
    intptr_t logstep = bsr(n);
    intptr_t step = intptr_t(1) << logstep;
    int pivot = arr[pos + step];
    while (step > 1) {
        intptr_t nextstep = step >> 1;
        int pivotL = arr[pos + nextstep];
        int pivotR = arr[pos + step + nextstep];
        pos = (pivot < key ? pos + step : pos);
        pivot = (pivot < key ? pivotR : pivotL);
        step = nextstep;
    }
    pos = (pivot < key ? pos + step : pos);
    return pos + 1;
}

The idea turns binary search into something similar to quaternary search:

int quaternary_search_branchless (const int *arr, int n, int key) {
    assert((n & (n+1)) == 0); //n = 2^k - 1
    intptr_t pos = MINUS_ONE;
    intptr_t logstep = bsr(n) - 1;
    intptr_t step = intptr_t(1) << logstep;
    while (step > 0) {
        int pivotL = arr[pos + step * 1];
        int pivotM = arr[pos + step * 2];
        int pivotR = arr[pos + step * 3];
        pos = (pivotL < key ? pos + step : pos);
        pos = (pivotM < key ? pos + step : pos);
        pos = (pivotR < key ? pos + step : pos);
        step >>= 2;
    }
    pos = (arr[pos + 1] < key ? pos + 1 : pos);
    return pos + 1;
}

Both of these implementations are included into extended performance comparison given below. The binary search with preloading (binary_search_branchless_pre) actually becomes significantly faster in latency, sacrificing some throughput. The quaternary search is not so good.

Hybrid search

I tried to perform branchless binary search until the segment of interest becomes small enough, then use linear search within it. It seems that making several iterations of linear search is not a good idea though: in fact, the best way is to make the length of linear search fixed, so that it could be fully unrolled. That's why I stopped on doing 16-element linear search. Using movemask instead of counting seems to be a bit faster in this case:

int hybridX_search (const int *arr, int n, int key) {
    intptr_t pos = MINUS_ONE;
    intptr_t logstep = bsr(n);
    intptr_t step = intptr_t(1) << logstep;
    while (step > 8) {
        pos = (arr[pos + step] < key ? pos + step : pos);
        step >>= 1;
    }
    pos++;
    step <<= 1;

    __m128i vkey = _mm_set1_epi32(key);
    __m128i cnt = _mm_setzero_si128();
    __m128i cmp0 = _mm_cmpgt_epi32 (vkey, _mm_load_si128((__m128i *)&arr[pos+0]));
    __m128i cmp1 = _mm_cmpgt_epi32 (vkey, _mm_load_si128((__m128i *)&arr[pos+4]));
    __m128i cmp2 = _mm_cmpgt_epi32 (vkey, _mm_load_si128((__m128i *)&arr[pos+8]));
    __m128i cmp3 = _mm_cmpgt_epi32 (vkey, _mm_load_si128((__m128i *)&arr[pos+12]));
    __m128i pack01 = _mm_packs_epi32 (cmp0, cmp1);
    __m128i pack23 = _mm_packs_epi32 (cmp2, cmp3);
    __m128i pack0123 = _mm_packs_epi16 (pack01, pack23);
    uint32_t res = _mm_movemask_epi8 (pack0123);

    return pos + bsf(~res);
}

It actually helped to reduce both throughput and latency time a bit (see plots below).

Compiler issues

1. mttd pointed out that there is intrinsic __builtin_unpredictable in Clang, which helps a lot in getting cmov instructions generated. I guess it is not present in GCC and MSVC...
2. I created an issue for Visual C++ about that stupid "or r9, -1" instruction generated. UPDATE(Nov.2017): this transformation is disabled when compiling for speed, the fix is targeted for version 15.6.

Extended performance results

Since all the added implementations are for binary search, the best plot would be the one which draws time per search divided by log2(N), which is something like "time per iteration of simple binary search":

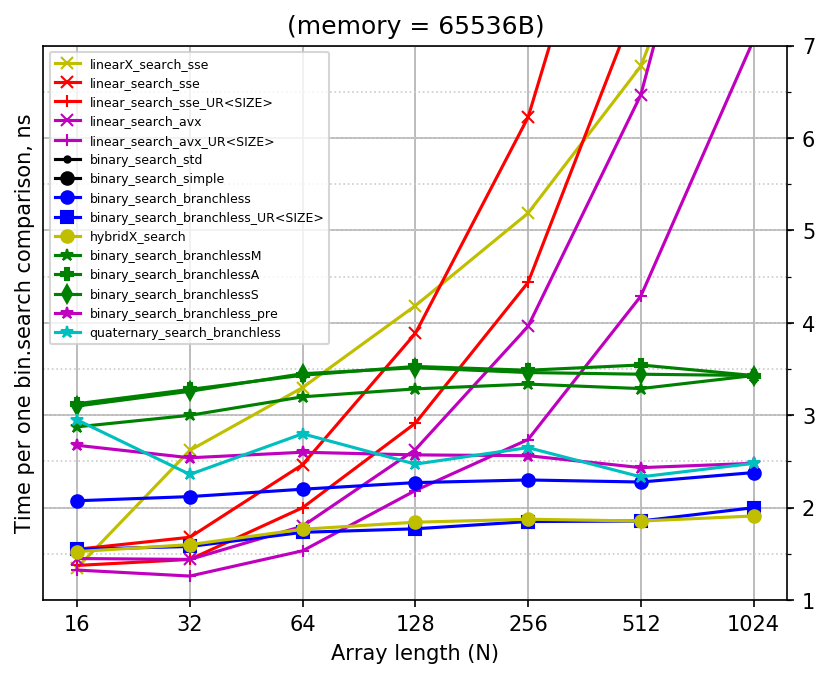
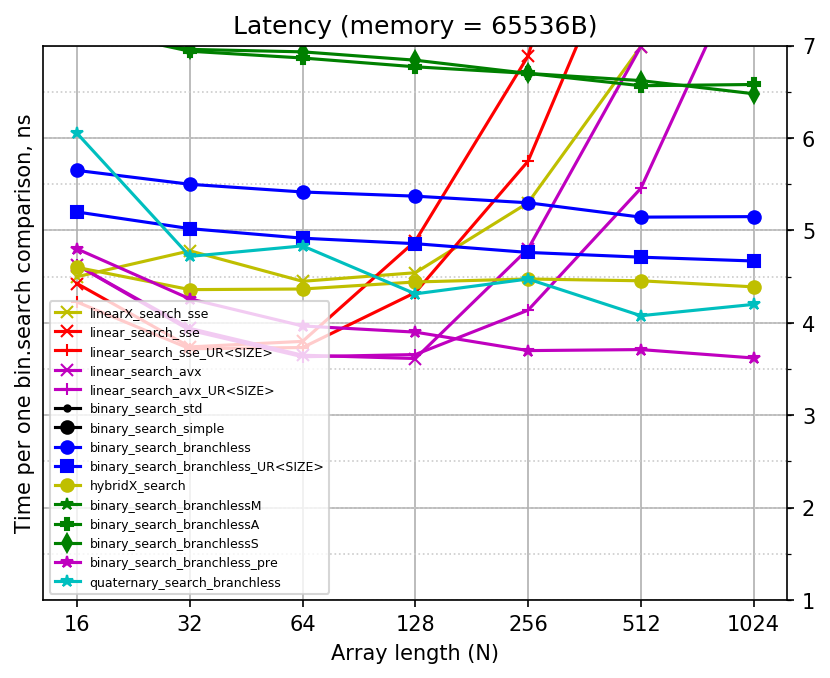
Here is the plain plot also:

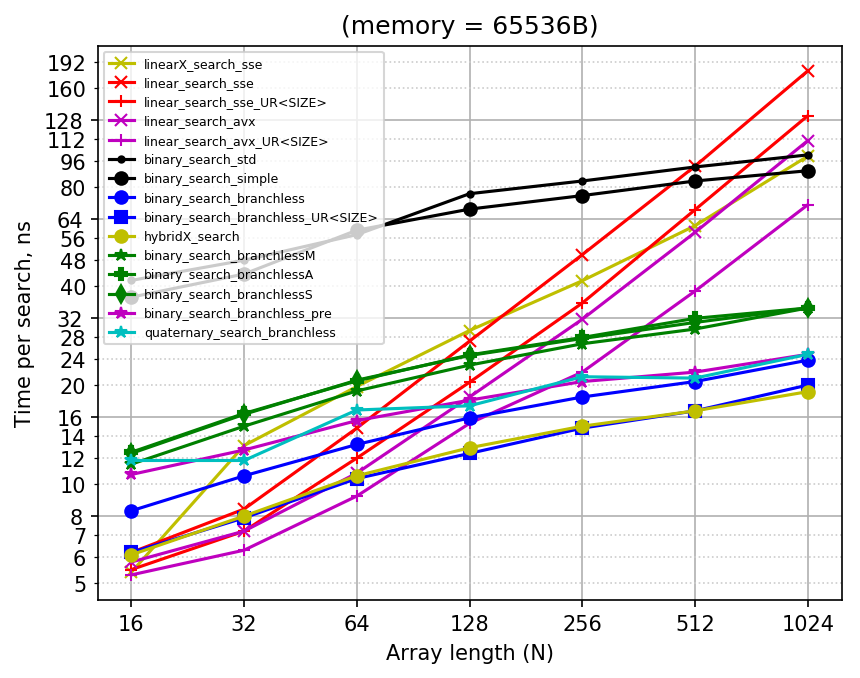
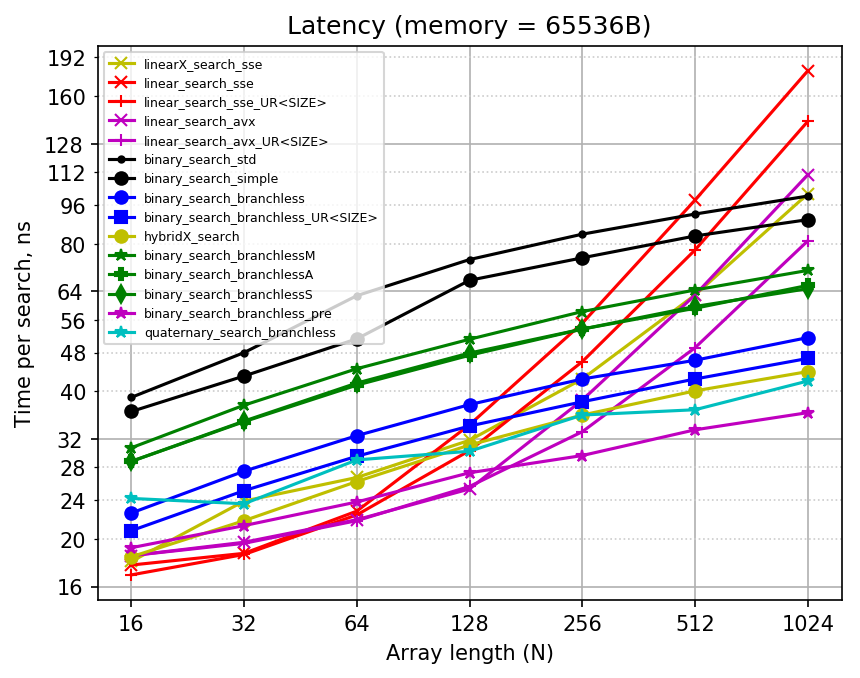
Sorry for the mess: there are too many implementations being compared already. Note that linear searches now use cross style of markers, while binary searches use solid figures or asterisks for markers.

The updated code including all new implementations is in the same repository as before.

Raw results are also available there in a branch. For instance, you can see all the text logs for throughput here and all the text logs for latency here.